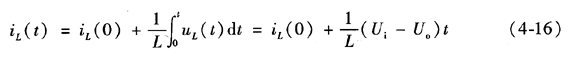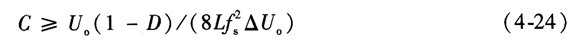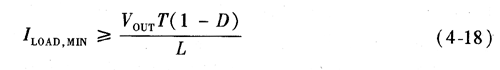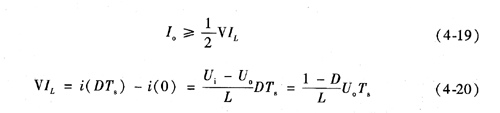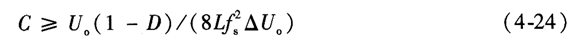Buck变换器电机控制系统

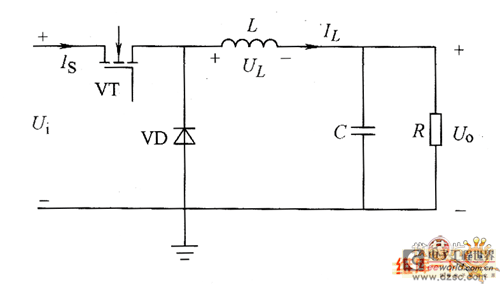
　　关键字：Buck 变换器 电机控制系统

　　按变换功能分，DC－DC变换器分为两种：一种是电压－电压变换器，一种是电流－电流变换器。磁悬浮控制力矩陀螺用高速永磁无刷直流电机的调速要求是 直流侧电压随电机转速变化而改变，因此这里采用电压ˉ电压的Buck降压变换器。若需扩展调速范围，则可采用Buck￣Boost或Cuk变换器。

　　Buck变换器、BuckˉBoost变换器和Cuk变换器工作中都存在着两种导电模式，即连续导电模式和不连续导电模式。连续导电模式是指在一个周 期中能量传递电感电流或能量传递电容电压总是大于零，即电感电流或电容电压是连续导电的；不连续导电模式是指在一个周期中电感电流或电容电压有一段时间为 零，即它们在一个周期中导电是不连续的。本节在后续的介绍中只讨论电感电流连续导电的情况。

　　Buck变换器是PWM型DC-DC变换器中最简单，也是最基本的一种，其电路拓扑如图1所示。

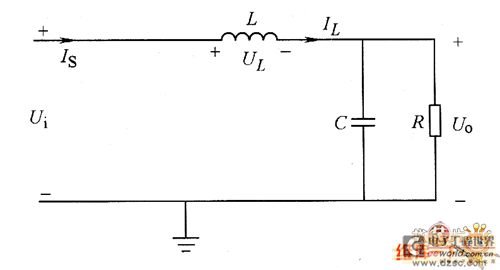
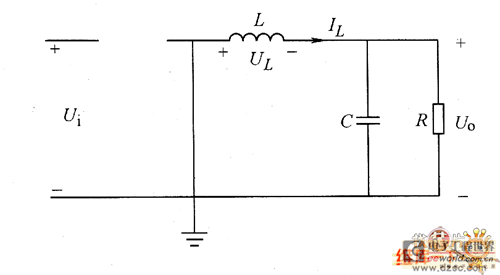
　　其工作原理是当VT导通时，二极管VD截止，其等效电路如图2所示。电源Ui通过能量传递电感乙向负载R送入能量，同时使电感L能量增加；当VT截止 时，电感释放能量使续流二极管VD导通，其等效电路如图3所示，在此阶段，电感乙把前一阶段增加的能量向负载放出，使负载电压极性不变并且比较平直。c是 滤波电容，它使输出电压的纹波进一步减小。从原理上说，此电容可去掉，只要电感L足够大，输出电压就可较为平直，但加上不大的电容，既可使纹波显著减小， 还可减小电感量。

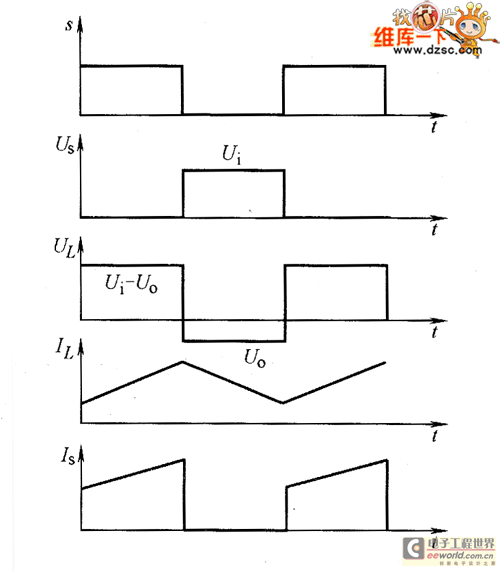
　　下面对Buck变换器控制系统进行稳态分析，从而求出该变换器的输入输出稳态电压比、电流变比和电感电流纹波等特性。

　　为分析稳态特性、简化推导公式的过程，作如下几点假定：

　　1）开关管、二极管均是理想元件，也就是指它们导通时电压为零，截止时电流为零，导通与截止的转换是瞬时完成的。    

　　2）电感、电容均为理想的，即 电感工作在线性区而未饱和，寄生电阻为零，而电容的等效串联电阻为零。

　　3）输出电压申的纹波电压与输出电压的比值小到允许忽略。

　　1．连续导电模式

　　在连续导电模式下，斩波器电感电流连续，电路分为两个状态，电路波形如图4所示。

　　当开关开通时，连续导电模式下电感中电流为

　　当开关管关断时，电路中主二极管、滤波电容、滤波电感组成回路。此时的电感电流为

　　2．不连续导电模式

　　Buck开关电路每次开通和关断时刻，电路电流正好为零，此时即为不连续导电模式，其电路波形如图5所示。

　　连续模式和断续模式指的流过电感中的电流有无中断。在断式模式变换器中，一个周期的某些时刻，流过电感的电流将为零。两种模式的电路状态也不相同，在连续模式下，最轻负载在所有时间段里，电路中一直都有电流流过。

　　式（4－18）为电路断续与连续的判别基本公式。其中，T为开关周期；D为占空比；L为滤波电感；VOUT为输出电压；ILOAD，MIN为最小输出电流，并假设整流器的正向压降要比输出电压小得多。

　　无论电路工作在连续模式还是断续模式下，关键是不要让变换器总处在负载变化的电路中，使其一会儿工作在连续模式，一会儿工作在断续模式，这样会使电路的稳定性变得较差。由式（4－18），其相类似的解释为负载中的电流平均值大于电感中的电流平均值，即

　　由式（4－19）和式（4－20）可知，基本Buck变换器连续导电与不连续导电

模式的临界条件为

式中，D为占空比；盂为开关频率；R为负载电阻。因此，变换器若要工作在连续导电模式下，必须满足式（4-21），则乙的最小值为

 　　对于LC滤波而言，负载与滤波电容C并联，高频状况下电感中大部分谐波电流都被C吸收了；L不能选的太小，否则会使电感电流脉动急剧增大，流过开关 管的最大电流也会增加，导致开关管的工作状态恶化。由此可知，L除了起滤波作用外，还有限制开关电流的作用。稳态时，乙的值决定了电感电流峰－峰值（也即 电感电流脉动）。假设允许的最大电感电流脉动为Δi，则有

　　因此，乙的值不仅要满足变换器工作在连续导电模式的要求，还要满足设计指标中电感电流脉动。

 　　3．输出滤波电容C的基本计算

　　根据输出电压纹波分量ΔUo和其他给定的设计数据，C的容量可以由下式求出：         

　　开关电源的输出滤波器是针对开关频率设计，截止频率一般取开关频率的1／10～1／100。由于对高速电机稳速在30000r／min时，要求有高精 度和快响应速度，这就对Buck环节输出电压提出了很高的要求，但对Buck环节输出电压的控制受其截至频率的限制，因此希望其有较高的截止频率。

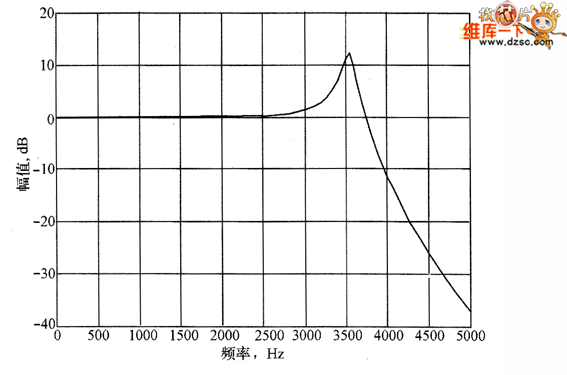
式中，f为截止频率；L为Buck环节滤波电感；C为Buck环节电容。

　　由式（4－11）可知为满足截止频率要求，电容、电感本应尽量减小，但由于本文所述电机电感量很小（仅有十几微亨），如果Buck环节电感过小，绕组 中波形振荡将较为严重。综合公式以上各式的计算与实际调试，并且希望整个电机系统能够有较快的响应速度，因此对于不同的电路参数，运用动态分析仪求得其相 应的传递函数。

　　当电机控制系统的Buck电路中，电感取值L=1.2mH、电容取值C=5.7μF时，利用动态分析仪得到相应的响应曲线，经过拟合后波形图如图6所示。

　　在进行高速电机系统的运动控制时，如果能够建立系统的相关模型，将对控制律设计控制参数选取提供有力依据，这也是系统设计的重要步骤之一。